pymc.Interpolated#
- class pymc.Interpolated(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#
Univariate probability distribution defined as a linear interpolation of probability density function evaluated on some lattice of points.
The lattice can be uneven, so the steps between different points can have different size and it is possible to vary the precision between regions of the support.
The probability density function values don not have to be normalized, as the interpolated density is any way normalized to make the total probability equal to $1$.
Both parameters
x_pointsand valuespdf_pointsare not variables, but plain array-like objects, so they are constant and cannot be sampled.(
Source code,png,hires.png,pdf)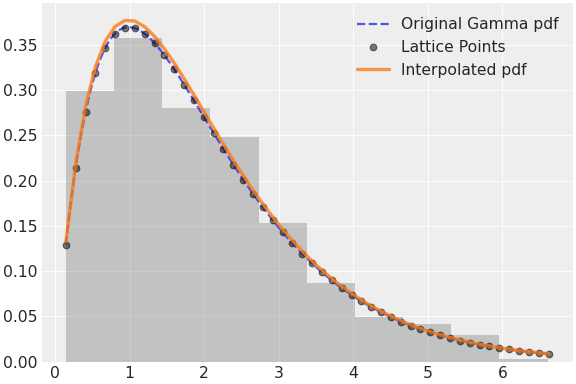
Support
\(x \in [x\_points[0], x\_points[-1]]\)
- Parameters:
- x_pointsarray_like
A monotonically growing list of values. Must be non-symbolic.
- pdf_pointsarray_like
Probability density function evaluated on lattice
x_points. Must be non-symbolic.
Methods
Interpolated.dist(x_points, pdf_points, ...)Creates a tensor variable corresponding to the cls distribution.