pymc.SkewNormal#
- class pymc.SkewNormal(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#
Univariate skew-normal log-likelihood.
The pdf of this distribution is
\[f(x \mid \mu, \tau, \alpha) = 2 \Phi((x-\mu)\sqrt{\tau}\alpha) \phi(x,\mu,\tau)\](
Source code,png,hires.png,pdf)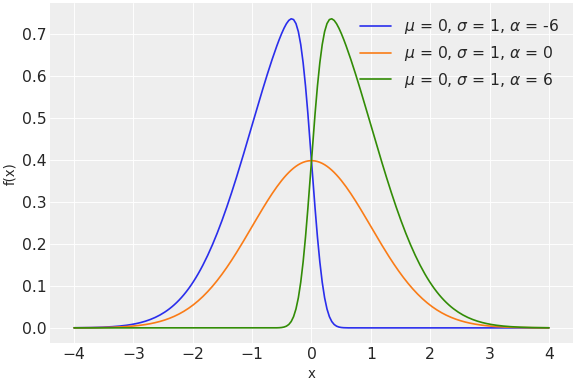
Support
\(x \in \mathbb{R}\)
Mean
\(\mu + \sigma \sqrt{\frac{2}{\pi}} \frac {\alpha }{{\sqrt {1+\alpha ^{2}}}}\)
Variance
\(\sigma^2 \left( 1-\frac{2\alpha^2}{(\alpha^2+1) \pi} \right)\)
Skew-normal distribution can be parameterized either in terms of precision or standard deviation. The link between the two parametrizations is given by
\[\tau = \dfrac{1}{\sigma^2}\]- Parameters:
- mutensor_like of
float, default 0 Location parameter.
- sigmatensor_like of
float, optional Scale parameter (sigma > 0). Defaults to 1.
- tautensor_like of
float, optional Alternative scale parameter (tau > 0). Defaults to 1.
- alphatensor_like of
float, default 1 Skewness parameter.
- mutensor_like of
Notes
When alpha=0 we recover the Normal distribution and mu becomes the mean, tau the precision and sigma the standard deviation. In the limit of alpha approaching plus/minus infinite we get a half-normal distribution.
Methods
SkewNormal.dist([alpha, mu, sigma, tau])Creates a tensor variable corresponding to the cls distribution.