pymc.StudentT#
- class pymc.StudentT(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#
Student’s T log-likelihood.
Describes a normal variable whose precision is gamma distributed. If only nu parameter is passed, this specifies a standard (central) Student’s T.
The pdf of this distribution is
\[f(x|\mu,\lambda,\nu) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})} \left(\frac{\lambda}{\pi\nu}\right)^{\frac{1}{2}} \left[1+\frac{\lambda(x-\mu)^2}{\nu}\right]^{-\frac{\nu+1}{2}}\](
Source code,png,hires.png,pdf)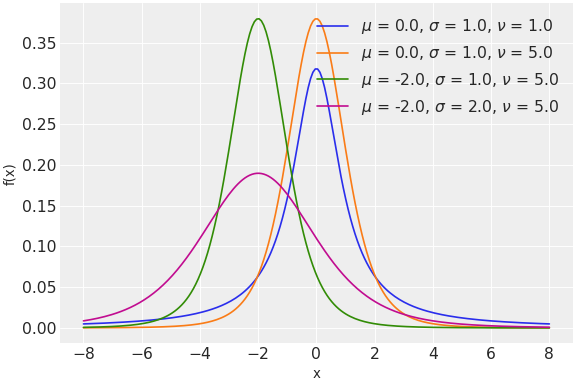
Support
\(x \in \mathbb{R}\)
- Parameters:
- nutensor_like of
float Degrees of freedom, also known as normality parameter (nu > 0).
- mutensor_like of
float, default 0 Location parameter.
- sigmatensor_like of
float, optional Scale parameter (sigma > 0). Converges to the standard deviation as nu increases (only required if lam is not specified). Defaults to 1.
- lamtensor_like of
float, optional Scale parameter (lam > 0). Converges to the precision as nu increases (only required if sigma is not specified). Defaults to 1.
- nutensor_like of
Examples
with pm.Model(): x = pm.StudentT('x', nu=15, mu=0, sigma=10) with pm.Model(): x = pm.StudentT('x', nu=15, mu=0, lam=1/23)
Methods
StudentT.dist(nu[, mu, sigma, lam])Creates a tensor variable corresponding to the cls distribution.